関数電卓

今回はフリーテーマということで電卓のことでも書いてみよう。

電卓。

電卓の使い方や、どんなモノを選べばよいかなど、ここのサイトに
詳しいが、ここでは私の電卓に関する思いを述べてみたいと思う。

最近では携帯電話やスマートフォンにも初めからついていて
今更単独の電卓を買う人も少ない。

更に、どこに行ってもＰＣがある世の中。

ちょっと複雑な計算ならPCで表計算ソフトなり、数式処理システムなりを
起動したほうがずっと効率的だ。

しかし、ちょっとした計算など、使い慣れた電卓がいつも手元にあると
便利なばかりか、世界が広がったりするものである。

ガソリンを入れた時の車の燃費計算から、海外旅行時の為替レートの
計算、はたまた小絞りボケの計算など、ちょっと疑問に思った時や、目の前
にある問題解決に絶大なる力を発揮してくれる。

さて、そんな素晴らしい働きをしてくれる電卓であるが何を選べば良いのだろう。

使い勝手や長所、短所などから考えてみる。



一般的に、持ち歩くならスマホの電卓アプリかな。と思う。

今日び、スマホに音楽プレーヤー、デジカメに予備バッテリー等々、持ち歩く
電子ガジェットは増えるばかり。

この上さらにガジェットを増やすと、それこそバッグやポケットのどこに何を入れたか
わからなくなってしまう。

フューチャーフォンなどではハードウェアインターフェースの都合で、どうしても
使いやすい電卓インターフェースを構築できないが、スマホなら自由自在。

更に専用ハードウェアの電卓では実現できないようなインターフェースも構築できる。

ただ、やはりハード的なキーがないのは入力ミスが起きやすい。

仕事場の机の上や居間の片隅などには専用のハードウェアをおいておくほうが
色々と楽しかったりする。



さて、では入力方法は何が良いのだろう。

現在電卓の入力方法は大きく分けて標準入力、数式通り入力、
ナチュラルディスプレイタイプ、RPNと大きく4つのタイプになる。

まず、標準入力電卓。

ま、いわゆる昔からの電卓である。

上半分の関数キーを除けばたいてい誰でも操作できる。

単純な四則演算ならなんの問題もなくできるが、ちょっと複雑になってくると
メモリを駆使したり、ノートに書き留めたりと色々工夫しないと答えが出せ
なかったりする。

数式通り入力は現物を持っていないが、PCで数式入れるのとほぼ一緒。

ネストが多くなってくると開きカッコと閉じ括弧の数が合わなくなったりして
見通しが悪い。

入力に苦労が多いので一度入力した式を何度も評価するような用途に
向いていると思う。

次に書くナチュラルディスプレイタイプがあればいらない。

いわゆるひとつの下位互換?

ナチュラルディスプレイタイプ電卓

natural displayというのは多分カシオの登録商標だと思うが、この際細
かいことは無視する。

最近の電卓のトレンド。

カシオだけじゃなく、シャープや米国のTI（テキサス・インスツルメンツ）の
関数電卓もこの方式が主流になっている。

最大の特徴は数式をノートに書くように表示することが出来ることだ。

これならネストの間違いを起こすことはほぼ無くなる。

なんだかんだといってもやはり一番わかりやすい入力方法だと思う。

そして次がRPN入力電卓。

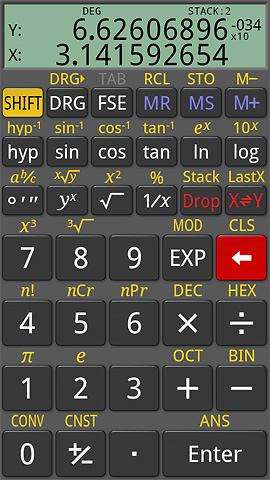
逆ポーランド記法とも言うが詳しくはここを参照してもらいたい。

演算する数値を先に入力しておいてあとから演算子（命令）を入力するタイプ。

一見わかりにくいが関数電卓に関して言えば四則演算も、三角関数や対数といった
関数も同じように扱えるため、通常タイプや数式通り入力のようなインターフェースの
矛盾が発生しない。

どういうことかというと、通常の関数電卓は四則演算は数式通り、その他の関数は
後置タイプのため、それぞれの機能が何に対して働くのかがばらばらになってしまっている。

RPN電卓はすべての演算コマンドは現在あるレジスタの値に対して機能する。

四則演算やy^x、→P等はXレジスタとYレジスタ。

三角関数や対数、メモリのSTOはXレジスタとあくまでも現在あるレジスタに機能するが
標準入力タイプや、数式通りは現在の表示レジスタであったり、演算結果だったりと
統一されていない。

今ある国産関数電卓のインターフェースの矛盾の根源はここにある。

その他のネストを意識しなくていいとか、演算の優先順位の問題が基本的に
起こりえないなどの特徴は、実際は操作する人間が判断しつつ入力しているからで
けしてこの入力方法の利点とは言えないと思う。

それより操作する人間の判断を反映しやすいインターフェースということが重要なのだ。

と、理屈をこねくり回していてもわかりにくいと思うので、実際の問題を解きながら
それぞれの特徴を見ていきたい。

まず、上記の関数電卓マニアの部屋様のサイトにある問題をとりあげてみよう。

ナチュラルディスプレイは難しいことを考えずこのまま入力すればよろしい。

2 [√] [( ] [( ] [□/□] 1 [↓] 8 [→] [ )] [x^2] [＋] [( ] [□/□] 1 [↓] 12 [→] [ )] [x^2] [ )] [x^-1] [＝]

2とルートの間のかける記号は省略可。

大変わかり易い。

式の内容を知らなくても入力できるし、数字やネストの間違いにも気づきやすい。

また、数値を変えての計算もプレイバック機能で簡単。

やはり現代の主流と考えて良いと思う。

標準入力タイプは、メモリ使ったりとめんどくさいのでパスしてRPN電卓。

iPadアプリのHP-15Cで計算してみる。

8 [1/x] 12 [1/x] [g] [→P] [1/x] 2 [×]

以上である。

この数式、値の二乗を足して平方根をとっているので、直交座標、極座標変換で
出すことが出来る。

[→P]はXレジスタとYレジスタに入っているX座標とY座標を極座標のｒとθに変換する
関数。

座標変換はfx-913ESにも付いているが、ナチュラルディスプレイ機の場合そんな回りくどい
方法を取らないほうが良い。

せっかくの自然入力の意味がなくなってしまうからだ。

ところがRPN電卓の場合は、数式の意味を考えながら入力するのが楽しかったりする。

次に上記「関数電卓マニアの部屋」の管理人様、東海大学准教授遠藤雅守様の著書
「理系人のための関数電卓パーフェクトガイド」に載っている「ヘロンの公式」の問題をやってみる。

今回も標準入力タイプはパスしてナチュラルディスプレイ電卓。

やはり何も考えず式のとおり入力する。

まず、下の式でs(小文字)を求める。

[( ] 2 [＋] 3 [＋] 4 [ )] [÷] 2 [＝]

ナチュラルディスプレイ機にはAns機能がついていて直前の答えをAnsキーで利用できる。

[√] [Ans] [( ] [Ans] [−] 2 [ )] [( ] [Ans] [−] 3 [ )] [( ] [Ans] [−] 4 [ )] [＝]

括弧と括弧の間のかける記号は当然省略可。

見たまんま。

間違いようがない。

次にRPN。

下式はま、普通に・・・、

2 [Enter] 3 [＋] 4 [＋] 2 [÷]

次にこの答えをTレジスタに入れ上式を計算する。

[Enter] [Enter] [Enter] 2 [−] [×] [X⇔Y] 3 [−] [×] [X⇔Y] 4 [−] [×] [√]

HP-15Cのスタックは4段、X, Y, Z, Tとあり、通常計算で使われるのはXとY。

最上段のTレジスタに入った値はレジスタの数値が下降するときコピーされる
仕掛けになっているので無限に出てくる。

[X⇔Y]はXレジスタとYレジスタの値を入れ替える関数。

sからaを引いた値がXレジスタに入っていてYレジスタにはTレジスタから降りてきたsの
値が入っているので双方のレジスタの値を入れ替えXレジスタにsの値を入れる。

そしてsからｂの値を引いて先ほどの数にかける。

それを繰り返してルートをとれば答えが出る。

ま、いわゆるパズル感覚。

他人の作った問題ばかりでは申し訳ないので、先日計算した業務用2/3型ビデオカメラの
撮像素子の画素ピッチの計算をしてみる。

2/3インチというと本来25.4mm×2/3で16.9mmになるのだが、このサイズは2/3インチの
撮像管という意味で、その昔ビデオカメラがCCDでなく撮像管を使っていた頃の名残。

撮像面の対角線は2/3型で11mm、1/2型で8mm、1/3型で6mmとなる。

最近のビデオカメラの撮像素子は16:9になっているので対角11mmで16:9の撮像素子の
長辺の長さを求め、その長さを長辺の画素数1920Pixcelで割ってやればよい。

ナチュラルディスプレイ機で計算するにはまず計算式を求めておいて入力する方が間違いが
発見しやすいし、違う数値を入れての再計算もしやすいので計算式を作る。

で、これをそまま打ち込むと

[□/□] 11 [cos] [shift] [tan-1] [□/□] 9 [↓] 16 [ )] [ )] [↓] 1920 [＝]

カシオのナチュラルディスプレイ電卓の場合arctanとcosの閉じ括弧は分数でなければ
省略できるが、この場合省略不可。

RPN電卓の場合このように最初から数式がなくても適当に打っていけば答えが出る。

画面の縦横比が16:9なので

9 [Enter] 16 [÷]

直角三角形の偏角を求める

[g] [tan-1]

対角線の長さが11mmなので

11

直行座標変換

[f] [→R]

この時点でのXレジスタの値が撮像素子の長辺の長さなので長辺のピクセル数で割ると

1920 [÷]

これで答えが出る。

このように初めから数式のある問題を解く時には、見たまま打ち込めるナチュラルディスプレイ機が
優れているが、数式のない、いわゆる応用問題のようなものを解くときにはRPNが使いやすい。

解決すべき問題をそのまま打ち込めばいいのだ。

入れる数値の順番を間違えても入れ替えることができるし四段スタックを使いこなせば
数値の再利用も思いのまま。

このようにどちらが優れているかではなく、それぞれ得意な分野がある。

常に持ち歩く電卓にはRPN方式が適しているし、常に決まった公式の計算をする人は
ナチュラルディスプレイ機が使いやすい。

なら、両方、適材適所で使えばいいと言いたいところだが、使いなれない方の電卓を使うと
ついつい打ち間違いをしてしまう。

やはりどちらかに統一したほうがいい。

一般的に言えばナチュラルディスプレイかなー。

でも、複雑な計算や同じ数式の使い回しなどはPCを使ったほうが効率的だし、RPNの
軽快な操作感は麻薬のような甘美な魅力を秘めている。

私はやはりRPNを選んじゃう。

このページはWingWebに掲載されています。
WingWebが開いていない方はこちら。 WingWebを開く

2011.11.22 *** Hiroshi Yae -- E-Mail: h_yae@sa2.so-net.ne.jp -- Twitter: @h_yae ***